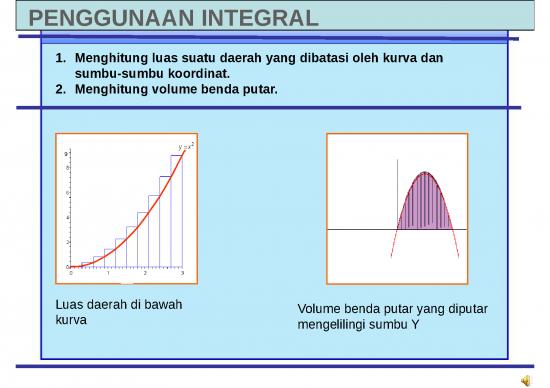
Integral Tentu                                                                                Luas Daerah
                                                                                  Luas 
                                                                                  Daerah
             Teorema Dasar Kalkulus 
             Teorema Dasar Kalkulus 
         Misalkan f adalah fungsi yang kontinyu pada selang [a, b] 
          Misalkan f adalah fungsi yang kontinyu pada selang [a, b] 
         dan misalkan F adalah anti turunan dari f pada selang 
          dan misalkan F adalah anti turunan dari f pada selang 
                      b
         tersebut, maka berlaku :
          tersebut, maka berlaku :
                       f(x) dx  F(b) F(a)
                      
                      a
         Untuk meringkas penulisan, F(b) – F(a) dinotasikan 
          Untuk meringkas penulisan, F(b) – F(a) dinotasikan                           b
                                                                                  F(x) a
         sebagai   
          sebagai   
          Contoh 1 :
          Contoh 1 :
                                 2       2
         Hitunglah nilai dari 
                                                  
                                    6x  4x dx
                                 
                                  1
         Jawab  
         Jawab  
                       2
                                                    =   2
                             2                 3    2
                           6x  4x dx
                                             2x  2x 1
                        1                             3        2         3
                                                    =  2(2)  – 2(2)  – [2(-1)  – 2(-
                          2
                       1) ]
          Home                                                                  Back        Next
                                                    =  16 – 8 + 2 + 2 = 12
                                                     
      Menghitung Luas dengan Integral                                                     Luas Daerah 
                                                                           Luas 
                                                                           Daerah
       Secara geometri definisi integral Riemaan di atas dapat 
       diartikan sebagai luas daerah di bawah kurva y = f(x) pada 
       interval  [a, b].              Berubah 
            Jumlah Luas                                     Integral
          y Partisi                   Menjadi           y
                                                                                  f(x)
                                 f(x)
                                      Tentukan limitnya 
                                            n  
                                                                        b
                         n                                                f(x)dx
                          f(x )x                                      
                        i1    i   i                                    a
                                       x                                              x
          0      a         x         b                 0      a                     b
                                  b                  n
                             L f(x)dxlim f(x)x
                                                          i    i
                                  a           ni1
          Home                                                            Back       Next
        Menghitung Luas dengan Integral                                                     Luas Daerah
                                                                                                  Luas 
                                                                                                  Daerah
          Kegiatan pokok dalam                                                                     x         yf(x)
                                                                       y                              i
          menghitung luas daerah dengan 
          integral tentu adalah: 
          1. Gambar daerahnya.
                                                                                                              f(x)
          2. Partisi daerahnya                                                                       L           i
                                                                                                      i
          3. Aproksimasi luas sebuah 
          partisi L   f(x) x
                         i         i      i
                                                                                                             x
          4. Jumlahkan luas  partisi                                  0                                xi   a
              L    f(x) x
                              i      i
                                                          a
          5. Ambil limitnya  L = lim  f(x) 
                                                   L f(x)dx
                                                            i
                                                          0
          xi                                                                                                  Next
            Home                                                                                Back
          6. Nyatakan dalam integral 
      Menghitung Luas dengan Integral                                                     Luas Daerah 
                                                                           Luas 
                                                                           Daerah
        Contoh 1.
        Contoh 1.
                                                                          2
       Hitunglah luas daerah tertutup yang dibatasi kurva y = x , sumbu x, 
      dan garis x = 3
        Jawab
        Jawab
       Langkah penyelesaian :                                                 f(x) x2
       1. Gambarlah daerahnya                   y
                                                                         xi
       2. Partisi daerahnya
       3. Aproksimasi luasnya L   x2 
                                         i     i
           xi
                                                                                  x2
       4.  Jumlahkan luasnya L                                                   i
                                         
           x2 x                                                           Li
            i     i
       5. Ambil limit jumlah luasnya
                                 3 2
                             L x dx                                            x
           L =  lim  x2 x 
                          i    i 0              0                           xi 3
                                    3 3     3
                                  x      3
       6. Nyatakan dalam integral 
                             L 3   3  09
                                     0
           dan hitung nilainya
          Home                                                            Back       Next
              Menghitung Luas dengan Integral                                                     Luas Daerah 
                                                                                                                                                                                                      Luas 
                                                                                                                                                                                                      Daerah
                     Contoh 2.
                     Contoh 2.
                                                                                                                                                                                                  2
               Hitunglah luas daerah tertutup yang dibatasi kurva y = x , sumbu Y, 
              dan garis y = 4
                     Jawab
                     Jawab                                                                                                                                                                                      f (x) x2
                   Langkah penyelesaian :                                                                                                                          y
                   1. Gambarlah daerahnya                                                                                                                 4
                                                                                                                                                                                     xi
                   2. Partisi daerahnya                                                                                                                                                                                  y
                   3. Aproksimasi luasnya L   
                            x.y                                                                                                                                                                                                            y
                                i
                   4.  Jumlahkan luasnya L    
                                                                                                        
                            y. y
                   5. Ambil limit jumlah luasnya
                                                                                       4
                                                                          L y.dy                                                                                                                                             x
                            L =  lim  y. y 
                                                                                                                                                            0
                                                                                      0
                                                                                                           4
                   6. Nyatakan dalam integral 
                                                                                     2             3                  2
                            dan hitung nilainya 2                                                                                            16
                                                                      L y   .8
                      Home                                                           3                                3                      3                                                   Back                          Next
                                                                                                           0