LKS Matematika Lanjutan 
                              
                                                                           BAB VII 
                                                     TRANSFORMASI GEOMETRI 
                              
                              
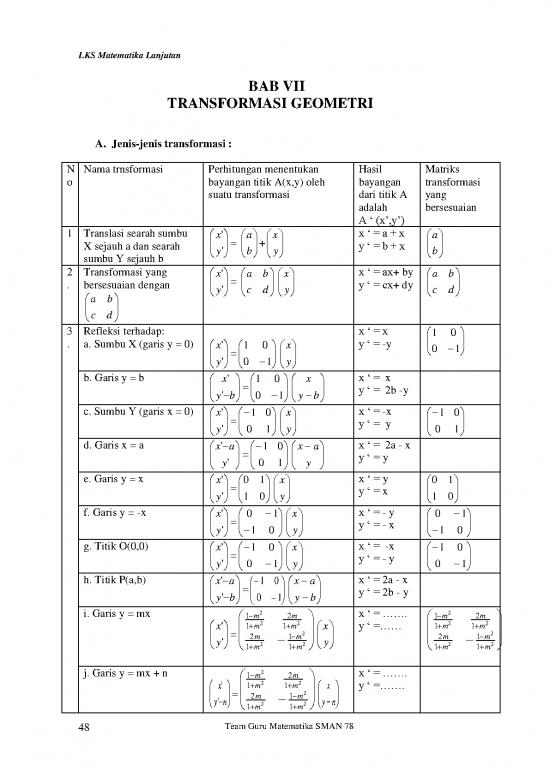
                                   A.  Jenis-jenis transformasi : 
                                    
                         N Nama trnsformasi                                 Perhitungan menentukan                                Hasil                   Matriks 
                         o                                                  bayangan titik A(x,y) oleh                            bayangan                transformasi 
                                                                            suatu transformasi                                    dari titik A            yang 
                                                                                                                                  adalah                  bersesuaian 
                                                                                                                                  A ‘ (x’,y’)  
                         1     Translasi searah sumbu                          x'         a        x                              x ‘ = a + x                a
                                                                                                                                                        
                               X sejauh a dan searah                              =      +                                  y ‘ = b + x                  
                                                                             y'       b y                                                            b
                               sumbu Y sejauh b                                                                                                         
                         2     Transformasi yang                               x'         a     b      x                          x ‘ = ax+ by               a     b
                                                                                                                                                               
                         .     bersesuaian dengan                                 =                                         y ‘ = cx+ dy                        
                                                                             y'       c      d  y                                                    c      d
                                 a     b                                                                                                                       
                                         
                                          
                               c      d
                                         
                         3     Refleksi terhadap:                                                                                 x ‘ = x                    1      0
                                                                                                                                                                      
                         .     a. Sumbu X (garis y = 0)                                                                           y ‘ = -y                             
                                                                               x'        1      0       x                                                             
                                                                                                                                                       0 1
                                                                                                                                                                      
                                                                                  =                   
                                                                             y'      0 1 y
                                                                                                     
                               b. Garis y = b                                    x'          1      0          x                  x ‘ =  x                 
                                                                                                               
                                                                                      =                                     y ‘ =  2b -y 
                                                                             y'b        0 1 yb
                                                                                                               
                               c. Sumbu Y (garis x = 0)                        x'        1 0           x                         x ‘ = -x                   1 0
                                                                                                                                                                
                                                                                  =                                         y ‘ =  y                             
                                                                             y'       0       1  y                                                    0       1
                                                                                                                                                                
                               d. Garis x = a                                  x'a          1 0           x  a                 x ‘ =  2a - x            
                                                                                                               
                                                                                      =                                     y ‘ = y 
                                                                             y'           0       1       y 
                                                                                                               
                               e. Garis y = x                                  x'        0 1          x                           x ‘ = y                    0 1
                                                                                                                                                              
                                                                                  =                                         y ‘ = x                            
                                                                             y'      1 0y                                                            1 0
                                                                                                                                                              
                               f. Garis y = -x                                 x'         0      1       x                       x ‘ = - y                   0      1
                                                                                                                                                                  
                                                                                  =                                         y ‘ = - x                               
                                                                             y'      1        0   y                                                 1        0 
                                                                                                                                                                  
                               g. Titik O(0,0)                                 x'        1 0             x                       x ‘ =  -x                  1 0
                                                                                                                                                                  
                                                                                  =                                         y ‘ = - y                               
                                                                             y'       0       1  y                                                   0       1
                                                                                                                                                                  
                               h. Titik P(a,b)                                 x'a          1 0          x  a                  x ‘ = 2a - x             
                                                                                                              
                                                                                      =                                     y ‘ = 2b - y 
                                                                             y'b         0     1  y b
                                                                                                              
                               i. Garis y = mx                                           1m2           2m                        x ‘ = …….                   1m2           2m
                                                                               x'      1m2           1m2  x                   y ‘ =……                  1m2           1m2 
                                                                                                           2                                                               2 
                                                                                  =      2m            1m                                                 2m            1m
                                                                                                                                                                             
                                                                               y'              2             2       y                                            2             2
                                                                                       1m             1m                                                1m            1m
                                                                                                                                                                                 
                                                                                                                                                           
                               j. Garis y = mx + n                                        1m2           2m                       x ‘ = …….                
                                                                               x'      1m2           1m2           x          y ‘ =……. 
                                                                                                           2         
                                                                                  =      2m            1m              
                                                                                                                     
                                                                              y'n             2             2      y  n
                                                                                        1m            1m             
                                                                                                                
                             48                                                          Team Guru Matematika SMAN 78 
                      LKS Matematika Lanjutan 
                   4   Rotasi                              x'     cos    sin      x           x ‘ = ….            cos    sin
                                                                                                                             
                   .   a. Rotasi dengan pusat                =                             y ‘ =……                             
                                                          y'   sin     cos   y                             sin      cos 
                           O(0,0) sejauh                                                                                     
                                           
                        
                       b. Rotasi dengan pusat             x'a      cos   sin    x  a        x ‘ = ….           
                                                                                   
                           P(a,b) sejauh                       =                           y ‘ = …… 
                                                         y'b   sin    cos  yb
                                                                                   
                   5   Dilatasi (perkalian)                x'     k    0    x                    x ‘ = kx            k   0
                                                                                                                    
                   .   a. Dilatasi pusat O(0,0)              =                             y ‘ =ky                   
                                                          y'   0 ky                                          0 k
                           dan factor skala k                                                                       
                        
                       b. Dilatasi pusat P(a,b)            x'a      k    0    x  a             x’-a =k(x-a)       
                                                                                
                           dan factor skala k                   =                          y‘-b =k(y-b) 
                                                          y'b    0 kyb
                                                                                
                       
                      Latihan 1 
                       
                                           a                                     2. Tentukan bayangan titik A(2,-1) oleh  
                                            
             1.       1. Translasi T =   memetakan A(4,-2)                         transformasi yang bersesuaian dengan  
                                          b
                                                                                              1     4
             2.           ke titik A’(2,3). Tentukan a dan b?                                            
                                                                                     matriks              ? 
                                                                                               3     2
                          Jawab :                                                                        
                                                                                     Jawab : 
                                                                                  
                                                                                  
                                                                                  
                                                                                  
                                                                                  
                                                                                  
                                                                                  
                                                                                  
                                                                                  
                                                                                  
                      3. Tentukan bayangan dari titik P(5,-3)                    4. Titik A’(5,7) adalah bayangan dari A  
                          oleh refleksi terhadap                                     oleh refleksi terhadap  
                      a. sumbu X                                                 a sumbu Y 
                      b. garis x + y =0                                          b. garis y = x  
                      c. titik O                                                 c. garis x = -3 
                      d. garis y – 2 = 0                                         d. titik (4,-1) 
                      e. garis x + 2y =0                                         e. garis 2x-y-3 = 0 
                          Jawab                                                      tentukan koordinat A pada tiap-tiap  
                                                                                     refleksi diatas ? 
                                                                                     Jawab :   
                                                                                  
                                                                                  
                                                                                  
                                                                                  
                                                                                  
                                                                                  
                                                                                  
                                                                                  
                                                                                  Team Guru Matematika SMAN 78                         49 
                  LKS Matematika Lanjutan 
                  5. Tentukan bayangan titik B(4,-2) oleh            6. P’(3,-2) adalah bayanga dari P  
                      rotasi sejauh 135 searah jarum jam            a. Karena dilatasi pusat O dan factor skala  
                      dengan pusat                                       2,  tentukan koordinat P ? 
                  a. O(0,0)                                          b. Karena dilatasi pusat R(-1, 2) dan factor  
                  b. P(-2, 6)                                            skala -2,  tentukan koordinat P ? 
                      Jawab :                                            Jawab : 
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                  7. Suatu rotasi dengan pusat O                     8. Suatu dilatasi memetakan A(2,1) dan  
                        memetakan titik A(-3,4) menjadi A’                 B(4,1) menjadi A’(4,7) dan B’(10,7). 
                        yang terletak tepat pada sumbu Y             a. tentukan Pusat dilatasi dan factor  
                        negative. Tentukan koordinat bayangan            skalanya? 
                        titik P(5,10) oleh rotasi tersebut ?         b. Tentukan bayangan titik (3,2) oleh  
                                                                         dilatasi tersebut ? 
                                                                         Jawab : 
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                                                                      
                   
                   
                   
                  50                                                          Team Guru Matematika SMAN 78 
                            LKS Matematika Lanjutan 
                             
                            B. Menentukan bayangan kurva y = f(x). 
                                 Langkah-langkahnya : 
                                 1. Dari rumus bayangan titik  nyatakanlah x dan y dalam x’ atau y’ 
                                                  x'         a        x                x          x'        a
                                                                                                   
                                      Bila           =      +  maka   =  -   
                                                 y'      b y                    y        y'     b
                                                                                                   
                                                  x'         a     b      x                x                         d      b       x'
                                                                                                 1                           
                                                     =                   maka  =                                               
                                                 y'      c      d  y                y        ad bc c              a   y'
                                                                                                                             
                                 2. Substitusikan x dan y ke y = f(x) kemudian hilangkan tanda aksen. 
                             
                            Latiha 2 
                             
                            1. Tentukan bayangan garis 2x – 3y + 1 = 0                                                                            a
                                                                                                                                                   
                                oleh transformasi yang bersesuaian                                      2. Tentukan translasi T =   yang  
                                                                                                                                                b
                                              1       4                                                                                           
                                                                                                                                                      2
                                dengan                      ?                                             memetakan parabola  y  2x 6x1  
                                             1       2
                                                                                                          menjadi  y  2x2 10x17  ? 
                                Jawab :                                                                     Jawab : 
                             
                             
                             
                             
                             
                             
                             
                             
                             
                             
                             
                             
                             
                            3. Tentukan persamaan garis yang                                            4.  Tentukan Pusat relasi dan besar sudut  
                                memetakan lingkaran                                                           putarnya sehingga memetakan garis  
                               x2  y2 2x4y 0   menjadi                                                    2x+y=3 menjadi garis 3x-y=2? 
                                lingkaran x2  y2  6x 8y  20  0?                                        Jawab : 
                                Jawab : 
                             
                             
                             
                             
                             
                             
                             
                             
                             
                             
                             
                             
                             
                             
                                                                                         Team Guru Matematika SMAN 78                                                        51