182x Filetype PDF File size 0.11 MB Source: mil.ufl.edu
EEL3135: Homework #1 Solutions
Problem 1:
(a) Explain the difference between a continuous-time and discrete-time signal.
A continuous-time signal xt() is a continuous functions of time t , a real-valued variable, while a discrete-
time signal xn[] is a function of time index n , an integer-valued variable; that is, a discrete-time signal is
only deÞned for a discrete number of points. Oftentimes, discrete-time signals are sampled versions of
continuous-time signals.
(b) Give at least one reason why the study of each type of signal (continuous-time and discrete-time) is
important.
Continuous-time signals exist in the real-world, and any discrete-time processing system (e.g. computer)
must interface with continuous-time signals both at the input and the output. Discrete-time signals have
grown in importance with the increased use of computers as digital signal processing (DSP) systems. As
such, both types of signals are important in understanding a complete signal processing system.
Problem 2:
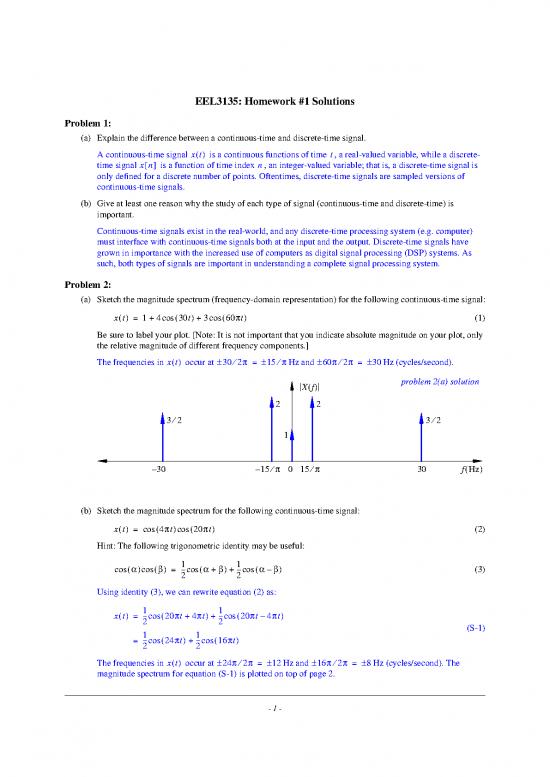
(a) Sketch the magnitude spectrum (frequency-domain representation) for the following continuous-time signal:
xt()= 14+ cos()30t + 36cos()0πt (1)
Be sure to label your plot. [Note: It is not important that you indicate absolute magnitude on your plot, only
the relative magnitude of different frequency components.]
The frequencies in xt() occur at ±30 ⁄ 2π = ±15 ⁄ πHz and ±π60 ⁄ 2π = ±30Hz (cycles/second).
Xf() problem 2(a) solution
2 2
32⁄ 32⁄
1
Ð30 Ð15⁄ π 0 15⁄π 30 f()Hz
(b) Sketch the magnitude spectrum for the following continuous-time signal:
xt()= cos()4πt cos()20πt (2)
Hint: The following trigonometric identity may be useful:
1 1
--- ---
cos()α cos()β= cos()αβ+ + cos()αβÐ (3)
2 2
Using identity (3), we can rewrite equation (2) as:
1 1
xt()= ---cos(20πt + 4πt) + ---cos(20πt Ð 4πt)
2 2 (S-1)
1 1
--- ---
= cos()24πt + cos()16πt
2 2
The frequencies in xt() occur at ±π24 ⁄ 2π = ±12Hz and ±π16 ⁄ 2π = ±8Hz (cycles/second). The
magnitude spectrum for equation (S-1) is plotted on top of page 2.
- 1 -
Xf() problem 2(b) solution
14⁄
Ð12 Ð8 8 12 f()Hz
Problem 3:
For the continuous-time signal xt()= 12+ cos()π ⋅ 50t + cos()2π ⋅ 80t , explain how the signal would be
changed by an ideal Þlter, whose frequency response is plotted below.
filter magnitude frequency response
2
1.5
1
0.5
0
-100 -50 0 50 100
f (frequency)
After the signal xt() is Þltered by the above ideal Þlter, the output yt() will be given by,
yt()= cos(2π⋅α50t + ) (S-2)
(Not enough information is given to determine α.) That is the DC component and 80Hz component will be
completely eliminated.
Problem 4:
(a) Compute the output sequence yn[], n ≥ 0, for the difference equation yn[]= xn[]Ð 3xn[]Ð 1 and the
input sequence xn[] plotted below.
6
xn[]
4
2
0
-2
-4
-4 -2 0 2 4 6 8 10
n
y[]0 = x[]0 Ð 3x[]Ð1 = Ð3 (S-3)
y[]1 = x[]1 Ð 3x[]0 = 13 (S-4)
- 2 -
y[]2 = x[]2 Ð 3x[]1 = Ð15 (S-5)
y[]3 = x[]3 Ð 3x[]2 = 14 (S-6)
y[]4 = x[]4 Ð 3x[]3 = Ð11 (S-7)
y[]5 = x[]5 Ð 3x[]4 = Ð15 (S-8)
y[]6 = x[]6 Ð 3x[]5 = 9 (S-9)
yn[]= 0, n≥7. (S-10)
This output sequence yn[] is plotted on top of the next page.
yn[]
10
5
0
-5
-10
-15
0 2 4 n 6 8 10
(b) Repeat part (a) for the following difference equation:
yn[]= Ðyn[]Ð1 +2xn[]Ðxn[]Ð1 (4)
and 0 ≤≤n 10. Assume y[]Ð1 = 0.
y[]0 = Ðy[]Ð1 + 2x[]0 Ð x[]Ð1 = Ð6 (S-11)
y[]1 = Ðy[]0 + 2x[]1 Ð x[]0 = 17 (S-12)
y[]2 = Ðy[]1 + 2x[]2 Ð x[]1 = Ð27 (S-13)
y[]3 = Ðy[]2 + 2x[]3 Ð x[]2 = 40 (S-14)
y[]4 = Ðy[]3 + 2x[]4 Ð x[]3 = Ð37 (S-15)
y[]5 = Ðy[]4 + 2x[]5 Ð x[]4 = 27 (S-16)
y[]6 = Ðy[]5 + 2x[]6 Ð x[]5 = Ð24 (note xn[]= 0, n > 5) (S-17)
y[]7 = Ðy[]6 + 2x[]7 Ð x[]6 = 24 (S-18)
y[]8 = Ðy[]7 + 2x[]8 Ð x[]7 = Ð24 (S-19)
y[]9 = Ðy[]8 + x[]9 Ð x[]8 = 24 (S-20)
y[]10 = Ðy[]9 + 2x[]10 Ð x[]9 = Ð24 (S-21)
This output sequence yn[] is plotted on the top of the next page.
- 3 -
40 yn[]
20
0
-20
0 2 4 n 6 8 10
Problem 5:
Assume you want to sample and Þlter the continuous-time signal xt()= sin()2πt ; further assume that the
discrete-time Þlter you want to apply to the sampled signal xn[] is given by the difference equation below:
1 1 1 1 1
--- --- --- --- ---
yn[]= xn[]+ xn[]Ð1 + xn[]Ð2 + xn[]Ð3 + xn[]Ð4 (5)
5 5 5 5 5
For which of the following sampling frequencies (samples/second) —1Hz, 3Hz, 5Hz and 7Hz —will the
output yn[] be zero for all n ?
The plot below shows the sequences that would be generated at the four different sampling frequencies. Note
that the Þlter in equation (5) will output zero for all n , if Þve consecutive samples of the input sequence
average to zero. This is the case for the 1Hz and 5Hz sampling frequencies, and is not true for the 3Hz and
1
7Hz sampling frequencies. Therefore, yn[] will be zero for sampling frequencies 1Hz and 5Hz.
1 1Hz 1 3Hz
0.5 0.5
0 0
-0.5 -0.5
-1 -1
0 5 10n 15 20 0 5 10 n 15 20
1 5Hz 1 7Hz
0.5 0.5
0 0
-0.5 -0.5
-1 -1
0 5 10 n 15 20 0 5 10 n 15 20
1. Note that in general, the 1Hz sampling frequency will not result in zero output, since we could easily
offset the sampling so that we would get a constant sequence of samples not equal to zero.
- 4 -
no reviews yet
Please Login to review.