Filetype PDF | Posted on 26 Jan 2023 | 2 years ago
Authentication
digital resources
158x Filetype PDF File size 2.97 MB Source: college.cengage.com
332522CB_1200_AN.qxd 4/26/06 6:23 PM Page 1
Precalculus with Limits, Answers to Section 12.1 1
Chapter 12 (d) 5
Section 12.1 (page 860)
Vocabulary Check (page 860) 0 5
0
1. limit 2. oscillates 3. direct substitution 3.
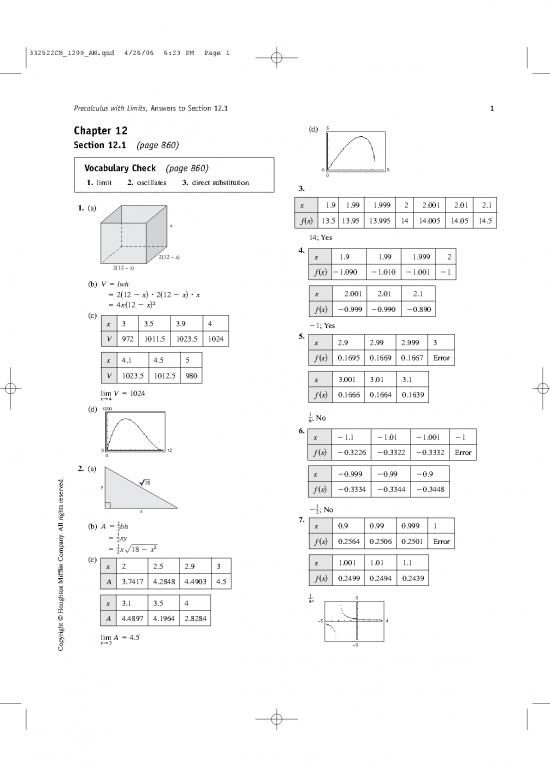
1. (a) x 1.9 1.99 1.999 2 2.001 2.01 2.1
x fx 13.5 13.95 13.995 14 14.005 14.05 14.5
14; Yes
2(12 x) 4. x 1.9 1.99 1.999 2
2(12 x) fx 1.090 1.010 1.001 1
(b) V lwh
212 x 212 x x x 2.001 2.01 2.1
2
4x12 x fx 0.999 0.990 0.890
(c)
x 3 3.5 3.9 4 ; Yes
1
V 972 1011.5 1023.5 1024 5. x 2.9 2.99 2.999 3
x 4.1 4.5 5 f x 0.1695 0.1669 0.1667 Error
V 1023.5 1012.5 980 x 3.001 3.01 3.1
lim V 1024 f x 0.1666 0.1664 0.1639
x→4
(d) 1200
1; No
6
6. x 1.1 1.01 1.001 1
0 12 f x 0.3226 0.3322 0.3332 Error
0
2. (a) x 0.999 0.99 0.9
y 18 f x 0.3334 0.3344 0.3448
x 1; No
3
(b) A 1bh 7. x 0.9 0.99 0.999 1
All rights reserved.2
. 1xy
2 f x 0.2564 0.2506 0.2501 Error
1 2
2x 18 x
(c) x 2 2.5 2.9 3 x 1.001 1.01 1.1
flin Company
A 3.7417 4.2848 4.4903 4.5 f x 0.2499 0.2494 0.2439
1; 3
x 3.1 3.5 4 4
Houghton Mif
A 4.4897 4.1964 2.8284 −5 4
lim A 4.5
Copyright © x→3 −3
332522CB_1200_AN.qxd 4/26/06 6:23 PM Page 2
Precalculus with Limits, Answers to Section 12.1 2
(Continued) 12. x 1.9 1.99 1.999 2
8. x 2.1 2.01 2.001 2 f x 0.0641 0.0627 0.0625 Error
f x 1.1111 1.0101 1.001 Error x 2.001 2.01 2.1
x 1.999 1.99 1.9 f x 0.0625 0.0623 0.061
f x 0.999 0.9901 0.9091 1; 2
1; 3 16
−3 3
−7 2
−2
−3 13.
9. x 0.1 0.01 0.001 0 x 0.1 0.01 0.001 0
f x 0.2247 0.2237 0.2236 Error f x 0.9983 0.99998 0.9999998 Error
x 0.001 0.01 0.1 x 0.001 0.01 0.1
f x 0.2236 0.2235 0.2225 f x 0.9999998 0.99998 0.9983
0.2236; 0.8 1; 2
−3 3 −3 3
−0.8 −2
10. x 3.1 3.01 3.001 3 14. x 0.1 0.01 0.001 0
f x 0.2485 0.2498 0.25 Error f x 0.050 0.005 0.0005 Error
x 2.999 2.99 2.9 x 0.001 0.01 0.1
f x 0.25 0.2502 0.2516 f x 0.0005 0.005 0.05
1; 2 0; 2
4
−4 2 −3 3
−2 −2
All rights reserved.
. 11. 15. y 16. y
x 4.1 4.01 4.001 4
8 3
f x 0.4762 0.4975 0.4998 Error 2
6
flin Company 4 x
x 3.999 3.99 3.9 21 123456
1
f x 0.5003 0.5025 0.5263 2 2
x 3
1 −2 2468 4
Houghton Mif2; 3 −2 5
−6 3 5 Limit does not exist.
Copyright © 17. 13 18. 12 19. Does not exist. Answers will vary.
−3 20. Does not exist. Answers will vary.
332522CB_1200_AN.qxd 4/26/06 6:23 PM Page 3
Precalculus with Limits, Answers to Section 12.1 3
(Continued) 59. (a) and (b) Answers will vary.
21. Does not exist. Answers will vary. 22. 1 60. Answers will vary.
23. 3 24. 3 61. (a) No. The function may approach different values from
the right and left of 2. For example,
0, x < 2
−3 3 −3 3 f x 4, x 2
−1 −1 6, x > 2
implies but
No. Answers will vary. Yes f 2 4, lim fx 4.
x→2
25. 2 26. 2 (b) No. The function may approach 4 as x approaches 2,
but the function could be undefined at x 2. For
−3 3 −3 3 example, in the function fx 4 sinx 2, the limit
x 2
is 4 as x approaches 2, but f2 is not defined.
−2 −2
x-
No. Answers will vary. Yes 62. As a function’s value approaches 5 from both the right and
left sides, its corresponding output values approach 12.
27. 3 28. 3
63. (a) 9
−1 8 −3 6
−3 12
−3 −3 −1
No. Answers will vary. No. Answers will vary. 6
29. 3 30. 6 (b) Domain: all real numbers x such that x ≥ 0
(c) Domain: all real numbers x such that x ≥ 0 except
−1 8 −6 12 x 9
(d) It may not be clear from a graph that a function is not
−3 −6 defined at a single point. Examining a function graph-
Yes will vary. No. Answers ically and algebraically ensures that you will find all
points at which the function is not defined.
31. 4 32. 4 64. (a) 4
−6 6 −4 8 −6 6
−4 −4 −4
Yes Yes 1
33. (a) (b) 9 (c) 1 (d) 6
All rights reserved.12 2 3 (b) Domain: all real numbers x except x 3
.
34. (a) 9 (b) 60 (c) 1 (d) 5 (c) Domain: all real numbers x except x ±3
2 5 (d) It may not be clear from a graph that a function is not
35. (a) 8 (b) 3 (c) 3 (d) 61 defined at a single point. Examining a function graph-
flin Company 8 8
36. (a) 2 (b) 0 (c) 0 (d) 2 37. 15 ically and algebraically ensures that you will find all
38. 6 39. 7 40. 9 41. 3 42. 2 points at which the function is not defined.
43. 9 44. 1 45. 7 46. 10 47. 1 65. 1, x 5 66. x 9, x 9
10 9 13 3 3
Houghton Mif48. 2 49. 3550. 3 51. e3 20.09 52. 1 5x 4 1 x 6
3 4 67. , x 68. , x 6
5x 2 3 x 1
53. 0 54. 0 55. 6 56. 3 57. True 69. x2 3x 9, x 3 70. x2 2x 4, x 2
Copyright ©58. True, provided the individual limits exist. x 2 x 2
332522CB_1200_AN.qxd 4/26/06 6:23 PM Page 4
Precalculus with Limits, Answers to Section 12.1 4
(Continued) 73. (a) 74. (a)
z (0, −4, 0)
71. (a) 72. (a) z −4
z z 4 −4 −2
−4 −2
(3, −3, 0) 2 −2 2
8 8 −2 4 −2 2
2 4
(3, 2, 8) 6 4 2 x y
(1, 0, 3) −2 4 −4
(3, 2, 7) (5, 2, 6) 4 x y −6
−4 −4
−4 −4 −4 −8
−2 −2 −6
−2 (0, 5, −5) (2, 0, −9)
2
4 4
6 4 4
x y x y (b) (b)
7 2 101
15 9 (c) 3, 1, 5 (c) 1, 2, 9
(b) 1 (c) (b) (c) 2 2 2
3, 2, 2 29 3, 1, 2
All rights reserved.
.
flin Company
Houghton Mif
Copyright ©
no reviews yet
Please Login to review.
